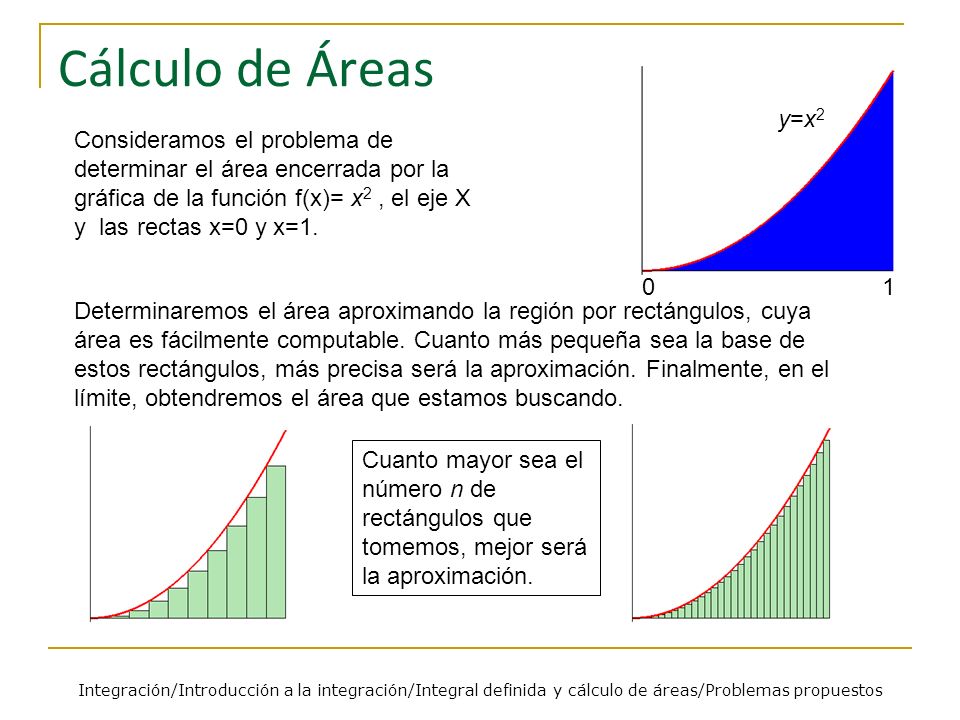
EL PROBLEMA AREA

EL PROBLEMA AREA

Así como la derivada es motivada por el problema geométrico de construir una tangente a una curva, el problema histórico que conduce a la definición de integral definida es el problema de encontrar un área. En específico, tenemos interés en la siguiente versión de este problema:

• Encontrar el área A de una región acotada por el eje x y la gráfica de una función no negativa continua y = f(x) definida sobre un intervalo [a, b].

El área de esta región se denomina área bajo la gráfica de f sobre el intervalo [a, b]. El requerimiento de que f sea no negativa sobre [a, b] significa que ninguna parte de esta gráfica sobre el intervalo está por abajo del eje x.

Antes de continuar con la solución del problema de área es necesario hacer una breve digresión para analizar una notación útil para una suma de números como

1 + 2 + 3 + … + n    & 1² + 2² + 3² + … + n² .

Notación sigma Sea a_k un número real que depende de un entero k.
 La suma a₁ + a₂ + a₃ + ...+ a_n se denota por el símbolo  esto es,

Puesto que ∑ es la letra griega mayúscula sigma, se denomina notación sigma o notación de suma. La variable k se denomina índice de la suma. Así,

es la suma de todos los números de la forma a_k cuando k asume los valores sucesivos k = 1, k = 2, . . . , y termina con k = n.

PROPIEDADES DE LA NOTACION SIGMA

La demostración de la fórmula i) es una consecuencia inmediata de la ley distributiva. Por supuesto, ii) del teorema se cumple para la suma de más de tres términos; por ejemplo,

FORMULAS DE SUMAS ESPECIALES

Para tipos especiales de sumas indicadas, particularmente sumas que implican potencias de enteros positivos del índice de la suma (como sumas de enteros positivos consecutivos, cuadrados sucesivos, cubos sucesivos, etc.) es posible encontrar una fórmula que proporcione el valor numérico verdadero de la suma. Para efectos de esta sección, centraremos la atención en las cuatro fórmulas siguientes.

Para n un entero positivo y c cualquier constante,

https://www.youtube.com/watch?v=TocqVkBzDrA
https://sites.google.com/site/calculointegralupaep/el-problema-del-area
http://www.fca.unl.edu.ar/Intdef/problemadelarea.htm
https://www.matesfacil.com/ejercicios-resueltos-integracion-areas.html